yaohaoyou

$\Large\color{red}\Diamond$ 是关键转化。

Fake Plastic Trees 2

首先有个比较简单的 dp，令 $f_{u,i,j}$ 表示 $u$ 子树内删了 $i$ 条边，目前 $u$ 连通块的大小为 $j$ 是否可行。

转移就类似树上背包合并，考虑如何优化 $j$ 这一维。

显然 $j$ 的最大值是 $T_u-iL$，最小值是 $T_u-iR$，其中 $T_u$ 表示 $u$ 子树内的 $A$ 和，所以 $j$ 的极差 $\le i(R-L)$。

接着证明对于 $j=x,y,z(x<y<z,z-x<R-L)$ 时，状态 $y$ 可以省略掉$\Large\color{red}\Diamond$，设选择了 $y$ 后最后形成的连通块大小为 $sz\in[l,r]$，则新增了 $sz-y$，分讨后可以证明 $sz-y+x$ 和 $sz-y+z$ 至少一个会 $\in [l,r]$，所以 $y$ 状态可以不计。此时所有记录的递增状态 $j_1,j_2\dots j_s$ 都满足 $j_{i+2}-j_i\ge R-L$，而又$\mathcal O(k)$ 个。所以状态只有 $\mathcal O(nk^2)$ 了，总复杂度为 $\mathcal O(nk^3)$。具体为什么不是 $\mathcal O (nk^4)$，是因为 $f_{u,i}$ 和 $f_{v,j}$ 卷的时候由于树上背包的证明是 $\mathcal O(nk)$ 的，剩余两个卷积是 $\mathcal O(k^2)$ 的。

P9266 [PA 2022] Nawiasowe podziały

令 $w(l,r)$ 表示区间 $[l,r]$ 中所有子串中合法括号序列数量，可以证明 $w$ 满足四边形不等式。令 $f_{i,j}$ 表示前 $i$ 个字符分成了 $j$ 段的方案数，则 $f_{i,j}=\min_{k<i}f_{k-1,j-1}+w(k,i)$，所以 $F(x)=f_{n,x}$ 为下凸函数。

套路地，显示使用 wqs 二分，然后需要求 $g_i=\min_{j<i}g_{j-1}+w(j,i)-mid$。因为 $w$ 满足四边形不等式，所以 $g$ 满足决策单调性，但 $w$ 不好直接求，并且 $g$ 求解过程需要在线。

发现 $w(l,r)$ 在做 $l\to l\pm 1$ 或 $r\to r\pm 1$ 时可以直接 $\mathcal O(1)$ 求解，所以可以用 cdq 分治套决策单调性分治解决，复杂度为 $\mathcal O(n\log^3n)$。但是可以使用LARSCH/简化 LARSCH（感觉像科技）算法优化至 dp 部分只要 $\mathcal O(n)/\mathcal O(n\log n)$，总复杂度为 $\mathcal O(n\log n/n\log^2n)$。$\Large\color{red}\Diamond$

简化 LARSCH 算法其实类似于 cdq 分治套决策单调性分治，令 $opt_t(x)$ 表示只考虑从 $[1,t]$ 的转移到 $x$ 的最优决策，$opt(x)=opt_{x-1}(x)$。具体过程是定义 $solve(l,r)$ 表示已知 $[1,l)$ 的 $g,opt$ 和 $opt_{l-1}(r)$，求解 $[1,r]$ 的 $g,opt$。

1. 用 $i\in [opt_{l-1},opt_{l-1,r}]$ 求出 $opt_{l-1}(mid)$，因为 $opt_{t}(x)\le opt_{t}(y)\le opt_{t}(z),x<y<z$。
2. 调用 $solve(l,mid)$。
3. 用 $opt(i),i\in [l,mid]$ 和 $opt_{l-1}(r)$ 求出 $opt_{mid}(r)$。
4. 调用 $solve(mid+1,r)$。

注意 1 操作中要移动 $w1$ 的指针，3 操作中要移动 $w2$ 的指针，可以证明整个过程中 $w1$ 和 $w2$ 的指针一共只会移动 $\mathcal O(n\log n)$ 次，若两种操作移动同一对指针会退化到 $\mathcal O(n^2)$ 次。

P6782 [Ynoi2008] rplexq

考虑对于每个点的度数和儿子子树大小根号分治，对于度数 $\le B$ 的点的询问考虑暴力枚举每个儿子，$>B$ 的点只有 $\mathcal O(\sqrt n)$ 个再考虑优化。$\Large\color{red}\Diamond$

记 $f(u,l,r)$ 表示 $u$ 子树中编号在 $[l,r]$ 的点的数量，则对于询问 $(l,r,x)$ 答案就是 $\binom{f(x,l,r)}2-\sum_\text{v is son of x}\binom{f(v,l,r)}{2}$。对于 $deg_x\le \sqrt n$，直接枚举 $v$ 后就会形成 $\mathcal O(n\sqrt n)$ 个求子树内编号在 $[l,r]$ 的数量的询问，把子树用 dfs 序拍掉就是 $\mathcal O(n)$ 个点 $\mathcal O(n\sqrt n)$ 次询问二维数点，离线后就是 $\mathcal O(n)$ 次单点加，$\mathcal O(n\sqrt n)$ 次区间求和，可以使用分块内记录块内和块间前缀和做到 $\mathcal O(\sqrt n)-\mathcal O(1)$ 修改/查询，复杂度为 $\mathcal O(n\sqrt n)$。但是空间还是 $\mathcal O(n\sqrt n)$，因为要存下 $\mathcal O(n\sqrt n)$ 个询问，可以发现 $x$ 的儿子的询问区间互不相交，所以可以扫描求完最小的区间后再把下一个加入，空间就是 $\mathcal O(n)$ 的了。

剩下考虑 $deg_x >\sqrt n$ 的怎么做。再次考虑分成两种情况，对于 $x$ 的儿子 $v$ 的子树大小 $>\sqrt n$ 的，$x$ 只会有 $\sqrt n$ 个这种儿子，可以理解为度数只有 $\sqrt n$，所以直接套用上面的做法即可。$\Large\color{red}\Diamond$对于 $v$ 子树大小 $\le \sqrt n$，直接暴力 $\mathcal O(siz_v^2)$ 枚举出所有二元组 $(x,y),x<y$，若满足 $l\le x< y\le r$ 就会贡献答案，这也是一个二维偏序（数点），但是现在有 $\mathcal O(n\sqrt n)$ 对修改，$\mathcal O(m)$ 个询问，使用 $\mathcal O(1)-\mathcal O(\sqrt n)$ 的分块处理即可。这部分的复杂度还是 $\mathcal O(n\sqrt n)$ 的，修改简单处理就可以做到线性空间。

总结一下就是直接对于每个点的儿子子树中前 $\sqrt n$ 大的做 $\mathcal O(\sqrt n) -O(1)$ 的二维数点，对剩余的做 $\mathcal O(1)-\mathcal O(\sqrt n)$ 的二维数点。

Omniscient Artist

首先将二维数点离线扫描线改成对 $a$ 做区间 $\pm 1$，由于 $a_i\le n$，所以 $m$ 的倍数只会有 $\mathcal O(\frac nm)$ 种。考虑以 $B$ 为块长做序列分块，区间加是好做的，由于初始时 $a$ 的差分数组都是 $c_i=0$，每次区间加会让 $c_l\gets c_{l}\pm 1,c_{r+1}\gets c_{r+1}\mp 1$，只会有 $\mathcal O(n)$ 次区间加，所以 $\sum |c_i|\le 2n$，所以每个块内的 $\max-\min$ 的和是 $\mathcal O(n)$ 级别的。询问时对每个块内枚举 $m$ 的倍数并查询出现次数即可，$m$ 的倍数一共只会有 $\mathcal O(\frac {\max-\min} m)$ 个，所以查询复杂度为 $\mathcal O(\frac n m)$，区间加复杂度为 $\mathcal O(\frac nB+B)$，平衡后整体复杂度为 $\mathcal O(n\sqrt n)$。注意重构的时候应该对每个块内的数删除而不是 $\mathcal O(\max-\min)$ 的清空，否则复杂度会退化到 $\mathcal O(n^2)$。

P14836 [THUPC 2026 初赛] 能量分配

这也太困难了。

$p\gets 317$，固定 $c$ 数组后，分配宝石的方案数就是 $\binom {n}{c_1,c_2,\dots c_m}$，由 Lucas 定理的过程可以得到 $\binom{n}{c_1,c_2\dots c_n}\not\equiv 0(\bmod p)$ 的必要条件是 $\forall k,\sum bit_k(c_i)=bit_k(n)$，其中 $bit_k(x)$ 表示 $x$ 在 $p$ 进制下的第 $k$ 位，即需要满足 $\sum c_i$ 求和过程中不能在 $p$ 进制下进位。$\Large\color{red}\Diamond$

先考虑 $n<p$，此时就只有一层。考虑直接枚举排序后 $c_i$ 之间的偏序关系，即相邻的两个位置之间的关系是 < 还是 =，一共只有 $\mathcal O(2^{m-1})$ 种。然后在确定相对偏序关系后，$\binom n {c_1,c_2\dots c_m}$ 的贡献和 $A,B$ 造成的贡献就独立了，分别考虑。$\Large\color{red}\Diamond$

先考虑求出 $A,B$ 的贡献。令 $dp_{S1,S2}$ 表示已经填入了集合 $S1$ 的选手，前面的偏序关系是 $S2$ 的贡献和，转移考虑枚举一个新的极长的相等段，选手编号集合为 $S3$，然后可以提前预处理出 $w_{S1,S3}$ 造成的贡献进行转移。复杂度为 $\mathcal O(\sum_{i=1}^m \binom{m}{i}\times 2^{i-1}\times 2^{m-i})=\mathcal O(4^m)$。

然后考虑求 $\binom{n}{c_1,c_2\dots c_m}$ 的贡献。由于 $c_i$ 的顺序不影响，所以这里只计算 $c$ 有序时的贡献和。令 $f_{i,j,S}$ 表示前 $i$ 个数和为 $j$，相对偏序关系为 $S$ 的总贡献，转移时讨论 $c_{i+1}$ 与 $c_i$ 的偏序关系。复杂度为 $\mathcal O(\sum_{i=1}^m 2^{i-1}p^2)=\mathcal O(2^mp^2)$。

拓展到 $n\ge p$，现在一共有 $\log_p n$ 层。类似上面的做法，将两种贡献分开计算，$A,B$ 造成的贡献直接 $\mathcal O(4^m)$ 预处理即可。考虑如何适应层数对偏序关系的影响。从高位到低位，原本相等的一段区间可能会分裂成几个有序的区间，考虑用 dp 记录这个过程。令 $f_{i,S}$ 表示到达 $i$ 层时的偏序关系为 $S$ 的方案数（$bit_2(S)=[c_i \ne c_{i+1}]$），考虑从 $f_{i,S}$ 转移到 $f_{i-1,S'}$（$S\sube S'$） 的转移系数 $g_{S,S',bit_{i-1}(n)}$，实际上 $g_{S,S',i}$ 可以将这个过程分成 $S$ 的每个 0 区间（等价类）变成 $S'$ 对应区间后对 $\sum bit_k(c)$ 维做卷积得来的。具体的，令 $h_{S,i}$ 表示相对偏序关系为 $S$，$\sum c=i$ 的方案数，则 $(S,S')$ 的转移可以通过 $h_{S,i}$ 的第二维 $i$ 的和卷积得来。$h$ 的转移和上一段落中的类似，$g$ 的状态中有许多可以通过记忆化解决$\Large\color{red}\Diamond$，比如下图中三个绿色段的相对顺序不会影响 $g$ 的值，所以可以将其排序后存入map进行记忆化。令map的大小为 $F(m)$，则预处理 $g$ 的复杂度为 $\mathcal O(F(m)p^2)$。若没有记忆化，$F(m)=3^m$（即枚举 $S\sube S'$），但是显然记忆化后会大幅减少状态数，实际上 $\color{red}F(12)=17547$。对于每次询问跑 $f$ 转移后记得最后与前面算的 $A,B$ 造成的贡献 $dp$ 拼起来。总复杂度为 $\mathcal O(4^m+F(m)p^2+q3^m\log_p n)$。

倒闭了，写不了一点，还要卡常，下播了。upd. 改完了。

最小乘积

由于 $A,B$ 很小，所以考虑直接枚举其中一个。令 $f_{u,i}$ 表示到 $u$ 时经过的 $\sum a=i$ 的最小的 $\sum b$，转移不难发现由于 $a_i>0$，所以这个转移是分层图，可以从小到大枚举 $i$ 后枚举每条边转移，复杂度为 $\mathcal O((n+m)mV)$，若没有发现分层图直接跑 dijkstra 会多一只 log 无法通过。

CF280D k-Maximum Subsequence Sum

由于 $k$ 和 $\sum k$ 很小，可以考虑模拟费用流。首先有个显然的费用流模型，对每个 $i$ 连边 $(S,i,1,0),(i,i+1,1,a_i),(i,T,1,0)$，还有 $k$ 的限制所以答案就是在这个图中增广 $k$ 次的最大花费。每次增广就是找到当前的最大区间和，然后将经过的链上的边反向并将费用变成相反数 $\Large\color{red}\Diamond$。这个过程可以使用线段树模拟，就是做最大子段和还有区间取相反数，复杂度为 $\mathcal O(q\log n+\sum kn\log n)$。

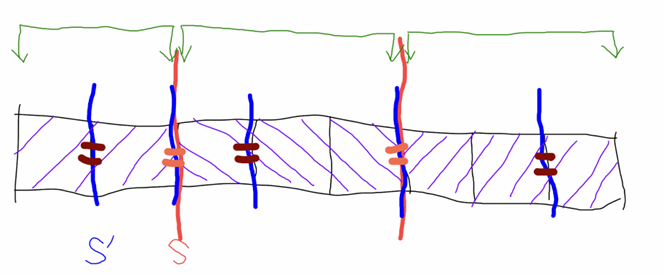
其实也可以从反悔贪心的方面思考刚刚的过程，就是先取当前和最大的区间 $[l,r]$，然后反悔再选取 $[l',r'] \sube [l,r]$ 并减去 $sum[l',r']$，这样区间就断成了 $[l,l')$ 和 $(r',r]$，完成了反悔操作，也就对应模拟费用流的反向弧的操作。

Poor Students

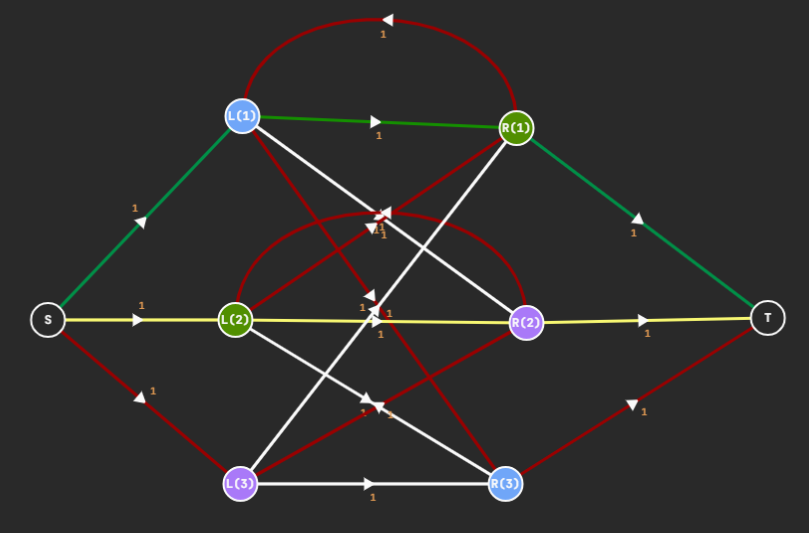
依旧是模拟费用流。首先这显然是一个带权二分图匹配问题，考虑建立费用流后如何优化。

如果手玩这个退流和走反向弧的过程不难发现每次实际上就是在右边选出一个序列 $p_1,p_2,\dots p_m$ 满足 $p[1,m)$ 都曾经被流满了（匹配完 $c_{p_i}$ 个左部点了），然后不断进行退流操作（即走反向弧）直到最后走到了一个没有流满的点 $p_m$ 后走到 $T$，下图红色的边就体现了退流的过程。由于 $m\le k\le 10$，所以考虑对右部点做一些本质的操作。$\Large\color{red}\Diamond$实际上每次寻找最短路时可以看作从 $p_i$ 走到 $p_{i+1}$，距离就是 $p_i\to x \to p_{i+1}$ 两条边的距离之和，这个可以提前预处理出任意两个右部点的 $x$ 的集合处理，所以就是已知任意两个右部点之间的距离求一条最短路 $rs\rightsquigarrow rt$ 且保证 $rt$ 没有流满。直接 $\mathcal O(k^3)$ 跑 floyd 即可，由于要模拟退流，所以要记录转移点来复原路径。复杂度为 $\mathcal O(nk^3+nk^2\log n)$。

CF1098F Ж-function

*3500。这种题写还是算了，太恐怖了一点。$\operatorname{Ж}(l,r)\to f(l,r)$

$f(l,r)=\sum_{i=l}^r|\operatorname{lcp}(s[l,r],s[i,r])|=\sum_{i=l}^r|\min(\operatorname{lcp}(s[l,n],s[i,n]),r-i+1)|$

由于 $\operatorname{lcp}(s[i,n],s[j,n])=\min_{k=rk_{i}+1}^{rk_{j}}ht_k$，所以考虑将 $i\in [l,r]$ 分成 $rk_i< rk_l$ 和 $rk_i>rk_l$ 和 $i=l$，然后将询问挂在 $rk_l$ 上。后面其实就是数据结构的事了。

$rk_i>rk_l$ 和 $rk_i<rk_l$ 是本质相同的，这里只讨论前者。区间最小值的拆贡献考虑离线后对 $rk$ 分治，令 $suf_i=\min_{j=i}^{mid} ht_j$，$pre_i=\min_{j=mid}^i ht_j$。从 $mid\to L$ 扫描线，当遇到询问 $[l,r]$ 时，令 $mn=suf_{rk_l}$，满足$\forall mid<i\le p,pre_i\ge mn$ 的 $p$ 最大，$mn$ 单调不降，$pre$ 单调不降，因此 $p$ 单调不降，考虑拆开贡献成 $\sum_{i=mid+1}^p [sa_i\in [l,r]]\min(mn,r-sa_i+1)+\sum_{i=p+1}^R[sa_i\in [l,r]\min(pre_i,r-sa_i+1)]$。前半部分是讨论对 $(sa_i,i)$ 的二维数点，扫 $p$ 的时候加入树状数组即可。后半部分当 $pre_i\le r-sa_i+1$ 时还需要满足 $sa_i\in [l,r],i\in [p+1,R]$，所以是对 $(i,sa_i,sa_i+pre_i)$ 的三维数点，考虑优化。题解做法是将限制拆成 $mn\le r-sa_i+1$ 加上 $pre_i\le r-sa_i+1< mn$，因为 $pre_i< mn$。第一个限制是二维数点，乍一看第二个限制还是三维数点，但是由于对于 $i\in (mid,p]$ 的都满足 $pre_i\ge mn$，所以就忽略掉了对 $i\in [p+1,R]$ 的限制也不会多算，所以就改成了二维数点。$\Large\color{red}\Diamond$其他的讨论都类似就算了。

复杂度为 $\mathcal O((n+q)\log^2n)$。