yaohaoyou

目前好像只会一些恰好选 $k$ 段的题目。

wqs 二分适用于解决对于一个上凸/下凸的函数 $g$ 在 $\mathcal O(D\log V)$ 的复杂度内求出一个单点值 $g(x)$，其中 $D$ 为求出 $\min/\max(g(x)-kx)$ 的复杂度，$V$ 为相邻 $g$ 上相邻两点斜率的范围。

具体的，我们需要使用一条直线 $l:y=kx+b$ 来切点 $(x,g(x))$，使得 $l$ 同时是凸包 $g(x)$ 的切线，求 $k$ 的最值，这是网络上常见的理解，我更愿意理解为找 $g'_k(x)=g(x)-kx+b$ 的最值。

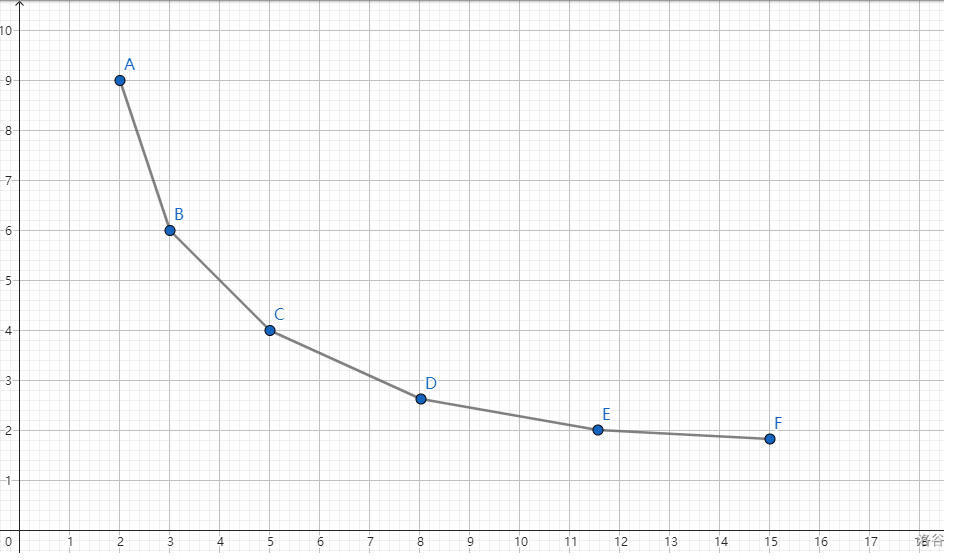
观察图像可知，当 $g(x)$ 为下凸包，$k$ 要求最大时，$g'_k(x)$ 会在 $[x,x+1]$ 时取到最小值，若二分 $k$ 时 $\operatorname{argmin}(g'_k(x))\le x$，则说明斜率过小（或刚好），将 $l=mid+1$，否则将 $r=mid-1$。$\operatorname{argmin}(f(x))$ 表示使函数 $f(x)$ 取到最小值的 $x$。（实际上应该求 $k$ 的最小值也是一样可以的。）

上凸包的情况类似，下面给几道题目。

P4983 忘情

首先要求的那个式子其实就是 $(\sum x_i+1)^2$。

令 $f_{i,j}$ 表示前 $i$ 个数分成 $j$ 段的答案，则有转移式 $f_{i,j}=\min_{k=0}^{j-1}(f_{k,j-1}+(s_i-s_{k}+1)^2)$，由于 $x_i>0$，可以证明 $f_n$ 是下凸的，要求 $f_{n,m}$。

这和上面的类似了，考虑对函数 $g(x)=f_{n,x}$ 做 wqs 二分。先二分一个斜率 $k$，然后需要判断 $g'(x)=g(x)-kx$ 在何处取到最小值。只需要将 $-kx$ 拆到每次新开一组的时候 $-k$ 即可。转移可以斜率优化。总复杂度为 $\mathcal O(n\log_2nV)$。

P6246 [IOI 2000] 邮局 加强版 加强版

令 $w(l,r)$ 表示区间 $[l,r]$ 放一个邮局的距离和，$f_{i,j}$ 表示前 $i$ 个村庄分 $j$ 段。可以发现 $w$ 满足四边形不等式，所以 $g(x)=f_{n,x}$ 为下凸函数。依旧套用 wqs 二分处理，check 时需要用决策单调性，可以使用二分队列。

CF2183H Minimise Cost

先贪心。子序列实际上可以转成从小到大排序后的子区间，负数尽量全部放一组，非正数首先选出部分组成 $k-1$ 组，剩余的和负数放一组。

依旧是一个类似的转移式，令 $f_{i,j}$ 表示前 $i$ 个数分为 $j$ 组，$w(l,r)=(r-l+1)(s_r-s_{l-1})$，$f_{i,j}=\min_{k=0}^{i-1} f_{k,j-1}+w(k+1,i)$。根据上面的贪心，只有在 $i=1 \vee a_i\ge 0$ 的时候需要转移枚举断电，对于 $w(l,r)(l=1\vee a_l\ge 0,a_r\ge0)$ 可以证明其满足四边形不等式，所以这个 $f$ 满足决策单调性，$f_n$ 是下凸的。

然后就和上面的 p6246 一样了。

P9266 [PA 2022] Nawiasowe podziały

令 $w(l,r)$ 表示区间 $[l,r]$ 中所有子串中合法括号序列数量，可以证明 $w$ 满足四边形不等式。令 $f_{i,j}$ 表示前 $i$ 个字符分成了 $j$ 段的方案数，则 $f_{i,j}=\min_{k<i}f_{k-1,j-1}+w(k,i)$，所以 $F(x)=f_{n,x}$ 为下凸函数。

套路地，显示使用 wqs 二分，然后需要求 $g_i=\min_{j<i}g_{j-1}+w(j,i)-mid$。因为 $w$ 满足四边形不等式，所以 $g$ 满足决策单调性，但 $w$ 不好直接求，并且 $g$ 求解过程需要在线。

发现 $w(l,r)$ 在做 $l\to l\pm 1$ 或 $r\to r\pm 1$ 时可以直接 $\mathcal O(1)$ 求解，所以可以用 cdq 分治套决策单调性分治解决，复杂度为 $\mathcal O(n\log^3n)$。但是可以使用LARSCH/简化 LARSCH（感觉像科技）算法优化至 dp 部分只要 $\mathcal O(n)/\mathcal O(n\log n)$，总复杂度为 $\mathcal O(n\log n/n\log^2n)$。

简化 LARSCH

简化 LARSCH 算法其实类似于 cdq 分治套决策单调性分治，令 $opt_t(x)$ 表示只考虑从 $[1,t]$ 的转移到 $x$ 的最优决策，$opt(x)=opt_{x-1}(x)$。具体过程是定义 $solve(l,r)$ 表示已知 $[1,l)$ 的 $g,opt$ 和 $opt_{l-1}(r)$，求解 $[1,r]$ 的 $g,opt$。

1. 用 $i\in [opt_{l-1},opt_{l-1,r}]$ 求出 $opt_{l-1}(mid)$，因为 $opt_{t}(x)\le opt_{t}(y)\le opt_{t}(z),x<y<z$。
2. 调用 $solve(l,mid)$。
3. 用 $opt(i),i\in [l,mid]$ 和 $opt_{l-1}(r)$ 求出 $opt_{mid}(r)$。
4. 调用 $solve(mid+1,r)$。

注意 1 操作中要移动 $w1$ 的指针，3 操作中要移动 $w2$ 的指针，可以证明整个过程中 $w1$ 和 $w2$ 的指针一共只会移动 $\mathcal O(n\log n)$ 次，若两种操作移动同一对指针会退化到 $\mathcal O(n^2)$ 次。